The Game of Life
and other
Cellular Automata
1

        Most people have a hard time recognizing feedback in the other methods of working with non-linear systems, but the feedback is easy to see in cellular automata. So, let's start the Game of Life!
        The Game of Life is over twenty-five years old. The original rules were designed by a mathematician by the name of John Conway and his students. You play the game on a grid of square cells that stretches in all direction to infinity. The game is a balancing act between life and death. A cell is alive if something is in it. Around each cell are its eight neighbors (four sides and four corners) that are either occupied by life or empty. If during a period of play, the occupied cell has exactly two neighbors everything stays the same. If three living cells surround an empty cell, they produce new life in the empty cell. If a living cell has four or more living neighbors, it dies of overcrowding. A cell also dies of loneliness if it has no neighbors or only one. All the births and deaths occur during the same generation or period of time. In the following period the life and death of cells are again decided. The game is started when a pattern of living cells is introduced on the grid. The game will then play itself over successive periods or generations until it is stopped.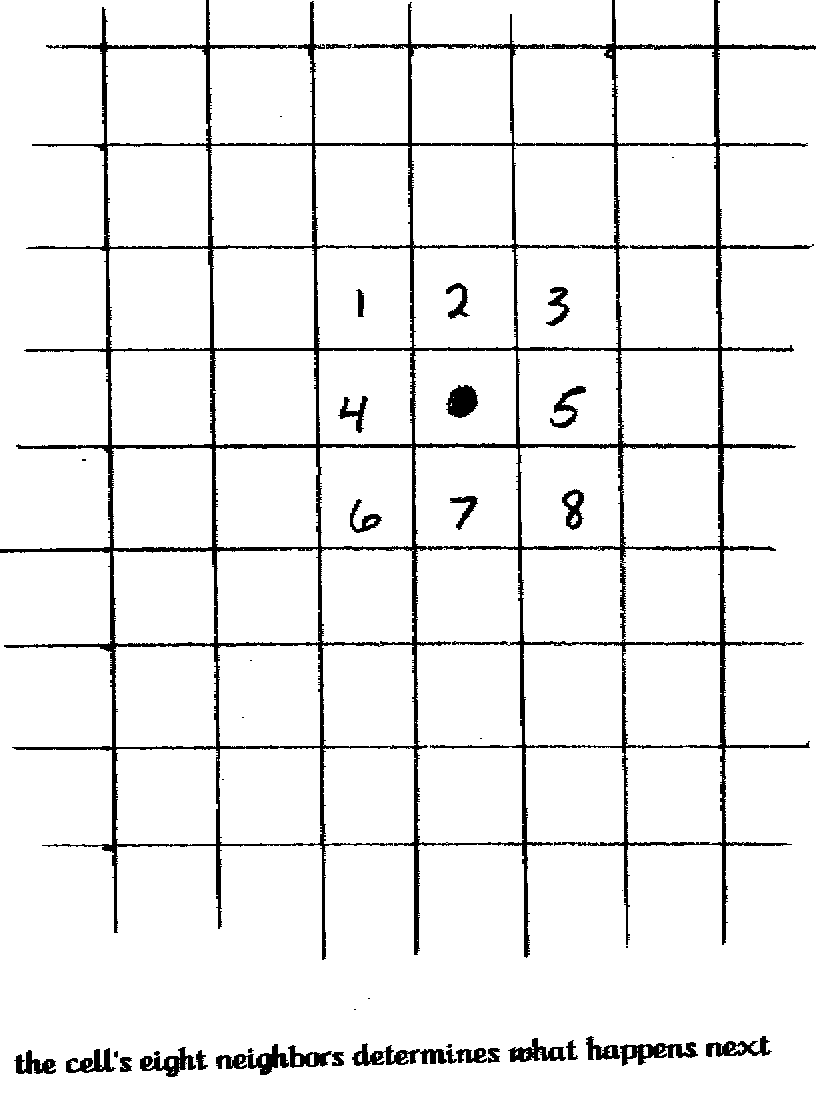
        The game sounds trivial, but among computer scientists and mathematicians it has taken on a cult status. Computers are well adapted on playing the game. The rules are simple, but repetitive and the grid is easy to generate, the perfect computer simulation. The patterns that can be generated by the game evolve unusual shapes and behaviors. Sometimes the patterns die out or degenerate into a static state. Some patterns pulsate with life. Some patterns form and then travel across the grid. Others form a colony and send offspring whistling across the board. In other words, the Game of Life can mimic on a small scale the life and death seen in the real world.
        I feel that one of the most interesting things discovered in the playing of Life is that more then one starting pattern can mutate into the same final pattern. 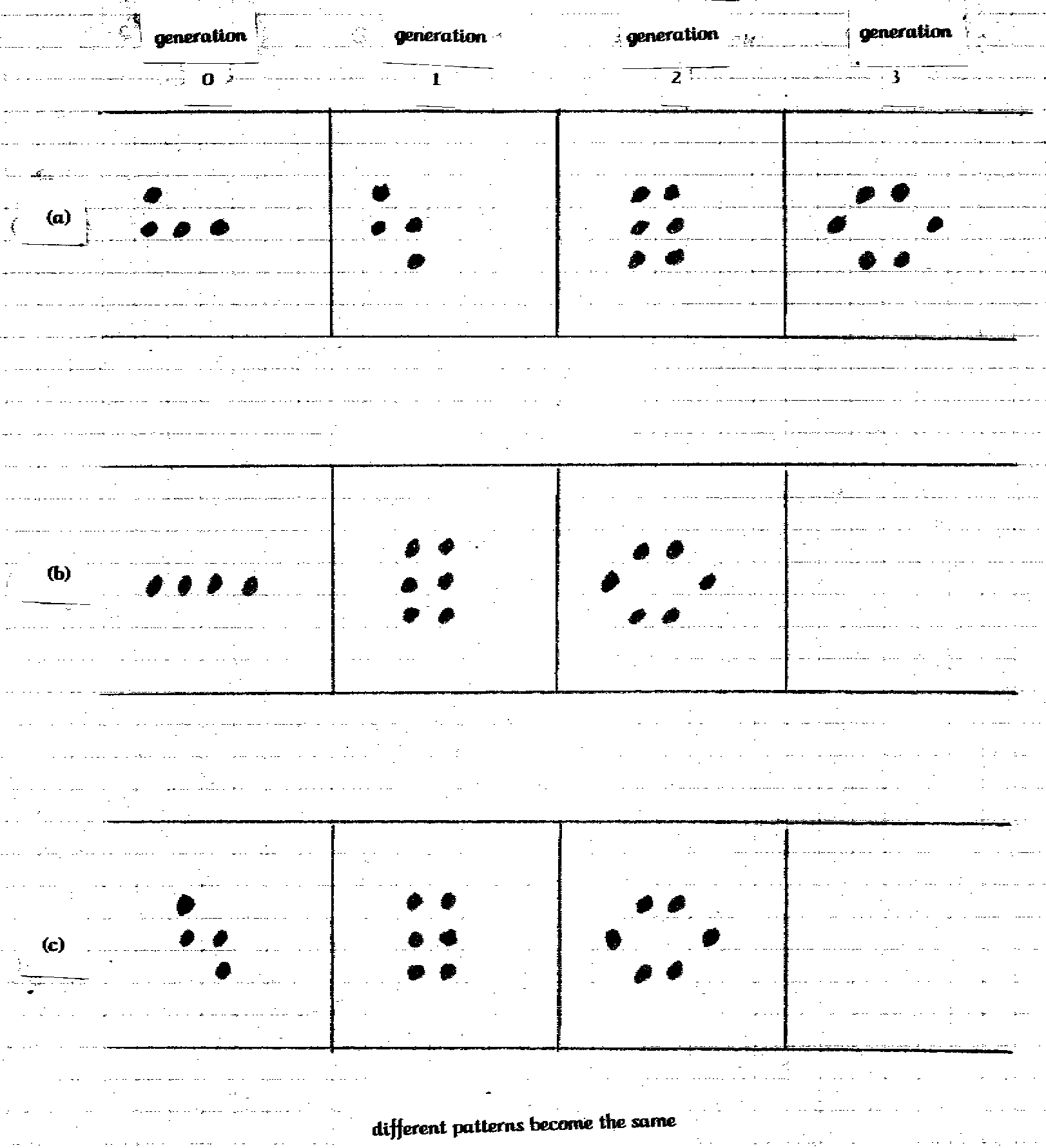The feedback on these few simple rules on cells can make it impossible to trace something back to its original condition. There is much more that can be discovered in the Game of Life, but it is time to go on to cellular automata in general.

2

        As with the Game of Life the idea of studying cells and rules is fairly new, in this case less then fifty years. In fact the Game of Life could be considered as a specialized version of cellular automata. Most cellular automata start with a grid and a set of rules on how and what to populate it with. Most of the time the top row of the grid is seeded with a starting pattern and the rules work down on each successive row to fill the grid. These rules and patterns can be used to mimic the formation of crystals, how molecules act in a turbulent flow, the spread of disease in a population, or infinitely many other real interacting systems.
        A mathematician by the name of Wolfram has done some interesting studies of cellular automata. If you are interested in the technical side of things, his study of patterns would be very helpful. Right now something he discovered about rules and patterns is quite interesting. A set of rules with different starting states will yield similar forms but differ in details. Also that different rules will generate different forms. What does this mean? If you have a set of rules (for example: biological genetic code) from different starting points you will get a similar final pattern or form. If you start with a biological group such as an insect and you get one that flies using flapping wings, you would expect flight with wings to again occur if you start with a different biological group. Dinosaurs developed into birds. Mammals developed bats. And so on.
        Now if we start with a different set of rules, let's say mechanical, the resulting forms should be different. In this case mechanical flight would not take place with flapping wings. It should have been expected that artificial flight should have developed other means, such as lighter than air balloons and fixed wings.
        Now my biological/mechanical example is a little extreme, but think of what happened. If you start with a set of rules dependent on feedback, different starting points will result in similar answers but with different details and different rules will make (generally) different answers.
        How does this help with other non-linear problems?
        It means that information from different problems that share the same rules or forms can be used to help understand each other. For example if people have collected data on a problem such as the weather patterns in Europe. How the patterns of weather change, but not the details, could be used to predict the weather in another location with similar rules such as the west coast of North America.
        It also means that if you are trying to solve a real life problem using a computer or machinery, don't be surprised if the most successful solution only has a passing resemblance to a real life answer. The converse is also true. If the computer or mechanical solution is similar to the real life answer, you have accidentally stumbled on a set of rules that are essentially the same as the real life rules.

3

        A mathematician by the name of Turing developed the idea of a universal mathematics machine. This Turing machine would be capable of judging the truth of any mathematical statement. The Turing machine could be imagined as a box that holds an action table or rules. Feeding through this box could be an infinitely log strip filled with squares that can be acted upon by the rules.
        Let's pretend that we have a very basic Turing machine that does just one thing, adding numbers. Encoded on the tape could be four 1's in successive squares to indicate the number 4. Those 1's would be followed by an empty space. The empty square would be used to stand for the operation of addition. Next on the tape would be six 1's for the number 6 and two blank spaces to indicate stop. The tape would be fed into the Turning machine and the action table would take over checking each square. It would read the 1's and continue on. When it got to the empty space it would fill it with a 1 and go on. When the next space is encountered it will go back one square and erase a 1. The result on the tape would be a series of ten 1's indicating that the answer is ten.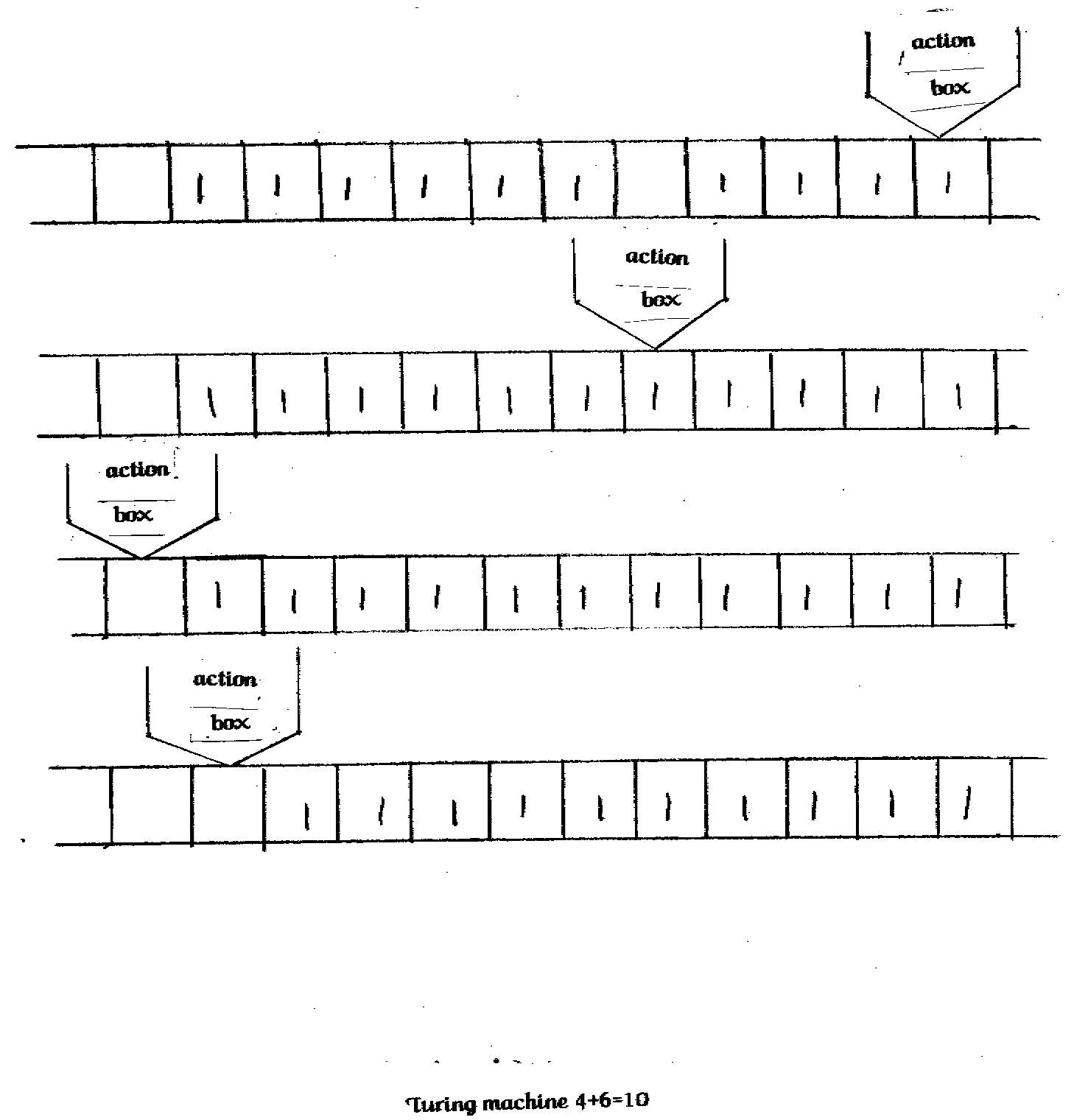
        Of course the action table for the mathematics we use would be enormous, so only simpler Turing machines have ever been used. What these machines have done is shown convincingly that simple rules can easily and quickly develop into very complicated systems.
        Guess what? Some of you may have already guessed what I am going to say next. The key is what you should have already learned about feedback and patterns. If you choose the correct set of rules and starting pattern in the Game of Life you can create a Turing machine. Rules, feedback, and similar patterns strike again!

Summery

Cellular Automata shows that simple rules can create complex systems and complex systems can be reduced to simple rules. Unfortunately because of the one way nature of the rules and feedback nothing is really that simple.




back to the intro        next section fractals

Back to the Keep's Gate