Complexity
1

        Complexity is to chaos as physics is to calculus. Complexity is a science. Chaos is a mathematical theory. You can use math in science. But science does not need to use mathematics to exist. Complexity is the science of any non-linear system at the fringes or edge of chaos. Remember the bifurcation graph I explained earlier?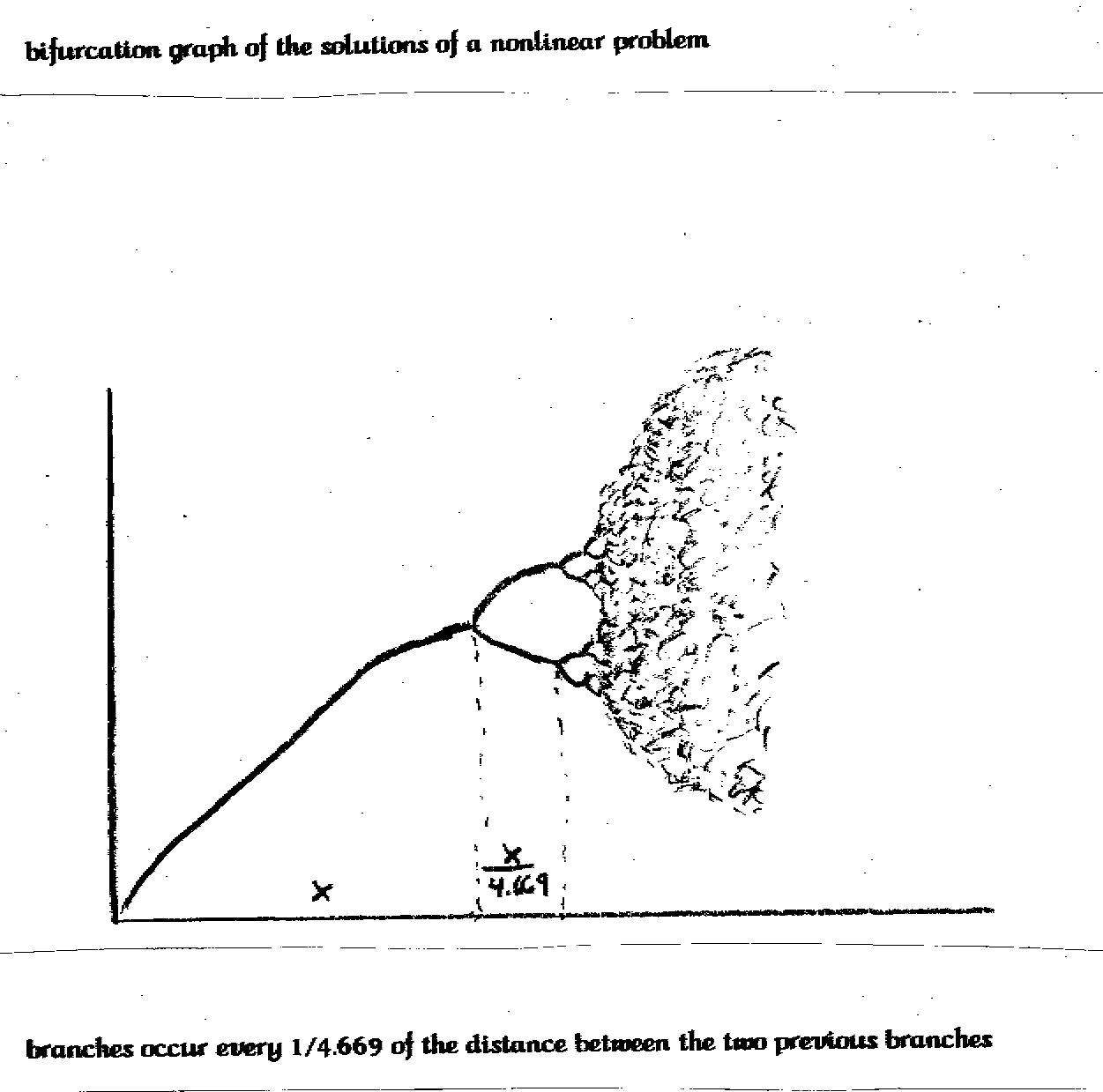 A problem can start out with answers that can be graphed as a line. It then can split or bifurcate into two lines and so on until there are so many lines a single answer has very little meaning. The science of complexity lives at the edge. The area that has more then one answer, but not the impossibly many.

2

        It's imaginary problem time. There is a small print shop that specializes in making charts and graphs. They have just received a few new printing contracts and had to hire a new employee. They try to run a single type of chart at a time; color pie charts, bar graphs, line graphs. Tomorrow they are going to run the week's line graphs. The new employee is given the job of loading the line graphs into the printing computers. The company is small and specialized. They use one program for making the line graphs and a second program to print the words and numbers using fancy typeface or fonts. In the final step of the process they merge the graph and words into a single page and print.
        The new employee does his job with just two minor problems. No one told him where to put the original information when he was finished and all the originals were accidentally thrown away. The second problem was that he forgot to link the text of each graph with their respective graph.
        The next day everyone shows up for work. The line graphs are perfect. The text looks great. But which text goes with which graph. They have text for earthquake fault activity on the West Coast. They have a graph of commodity prices for the Chicago Exchange. They have a disease survey for the CDC. A solar radiation chart from USC was on the computer. And finally a tree growth ring chart from the United States Forestry Department was present. Without the labels all the graphs looked the same.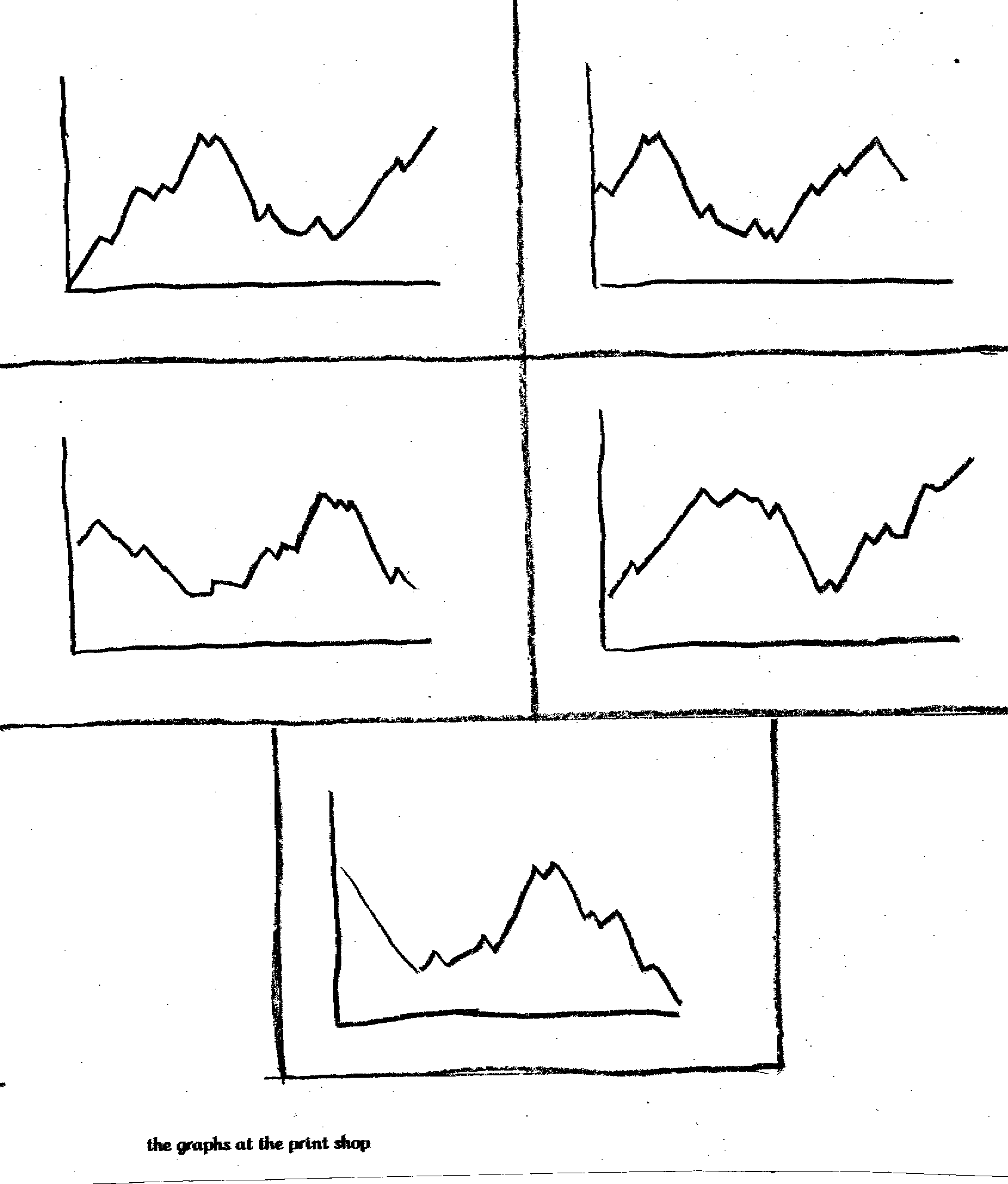
        About fifteen years ago a group of scientists and mathematicians who realized that the problems they were working on were also showing up in other fields got together. Why else would charts from such dissimilar problems look the same? There had to be a link in these dissimilar non-linear problems that produced similar results. Complexity was born.
        Complexity is more then a little bit unusual. It is a generalized science. You can use it to study the stock market or history, physics or psychology, biology or culture, or just about anything else with more then one stable solution. As a result you look for a general underlying form of the problem, the form that shows up across the different fields. Some people describe these forms as Meta rules. We have already talked about some Meta rules or underlying forms; Feigenbaum's number, similarity across scale,...
        Unfortunately the term Meta, which is used in words such as metaphysics, has a connotation of being mystical. Because the underlying form or rule is so generalized some scientists feel that the rules have to be so generalized as to be nearly useless. Others feel that what is now being done is akin to the mysticism of the Middle Ages.
        This generalization is more then a little neat. It is fun to see a problem that you are familiar with, in let's say economics, showing up in a biology paper. Anyone reading this who is familiar with just one non-linear problem should be able to understand those problems in completely different fields. Now back to the show.

3

        I would like you to consider a very basic non-linear system. A system that takes a completely random mixture and makes it organized. Imagine a pool of basic chemicals or elements. Add some energy and chemical bonding will occur. (Factors that will accelerate this process are catalytic action and phase change, but more on these later.) A successful chemical reaction will feed upon its success and organize more of the pool. Eventually it will organize the whole pool into a solution of repetitively bonding chemicals. Of course a disruption in the pool could result in a different chemical organization; i.e. a rock of nickel being thrown in.
        A catalytic action causes a change in bonding without changing itself. A catalytic agent can be a single chemical such as chlorine in the upper atmosphere that breaks down the ozone layer or a larger structure who's surface helps the bonding such as a car's catalytic converter. In our pool the catalytic agents would be both single and groups of chemicals and the clay structures around the pool. A catalytic reaction that results in a favorable condition for the agents causing the reaction will start to dominate the reactions in the pool (positive feedback). Guess what? We have a name for many of the chemical catalytic agents and compounds, proteins.
        Now all we need for a really neat system to be in place is something that could easily store and organize information. Our pool would then become really interesting. A phase change or a change of state will work beautifully.
        What are changes of state? We are made mostly of water and because of that we are very familiar with the changes of state of water. We think of water as a liquid, but if we start cooling a glass of water it will become a solid, ice. It has changed state or phase from liquid to solid. Of course there is another change we are familiar with when we put the glass in a microwave (liquid to gas), but right now I am more interested in the liquid to solid change.
        A fossil is a pattern frozen or stored in a solid form for millions of years. A solid can store information very well. If you look at something liquid, let's say a river, you will see that a liquid changes very easily. A liquid makes it easy to change information. What happens just at the edge of a phase change, a pool just about frozen with very small ice crystals floating across the pool. Some of the liquid will be frozen, information stored. Some of the liquid will stay fluid, information changing. Need to change some of the stored information, simply thaw. Need to store information, freeze. The bonding in our pool would now be able to store and change information.
        Do we have life generating from the pool? Current mathematical models indicate that we would. Consider your own body: mostly liquid with solids and semi-solid structures scattered throughout, mostly changing information with long term storage everywhere. Sounds like a possible match to me. (If you are interested in this topic check out some of the books I list at the end of this article. It would take too long to fully cover the idea here.)
        A basic idea about non-linear systems that this shows, is the ability of any system that has an energy flow and a means of selecting to organize completely random things. Think about what I just said: Energy flow -- means of selecting -- organized! Start with people, add goods (energy), get countries, towns, tribes. Start with plants and animals, add sunlight, get interdependent ecosystem. Start with good and services, add money, get stock market. Start with elements, add energy from big explosion, get galaxy. The means of selecting is built into the objects that are organized. People choose what they want. Animals survive or die. Elements can only combine in certain ways. Self contained organization of the random automatically occurring!

4

        Have you every played in the sand at a beach or in a sandbox with a child? Try to remember how the sand forms shapes.
        We have a large table in a room. Above the table we have tons of sand that we will slowly dribble onto the table. The sand will soon form mounds. Where the sand successfully bonds together there will be large mounds. Other areas will form plains or valleys. As you watch the sand build up you will see areas collapse at their sides. Sometimes a series of small slides, sometimes a large slide will happen. The most interesting and varies landscapes will occur at these sites. If you were trying to store information using the table, where could you store the most? The areas that form planes or the areas the have the slides. Notice that as long as there is structure to the sand, slides will occur. They can be small or large but they have to happen.
        The sand table is a simple model of a basic physical non-linear system. Slide patterns can be similar to earthquakes or volcanoes. The patterns can also be found in many other physical systems. But what is most interesting about the model is what it shows about systems we have previously thought of as not following physical models, biological and social systems. There is a danger here. This is where many of the problems with the misuse of these new methods of working with non-linear problems occur. The sand model shows were to first look and what to look for in studying a more complex non-linear problem. It doesn't guarantee what you will find. An answer to why is coming up in the next section.

5

        People are part of the animal kingdom. As part of the kingdom we are familiar with our other kingdom members. Take some time now and review in your own mind the relationship between physical characteristics and genes as you know it. Good. Now we will learn something different about genes and characteristics.
        Genes are one of the methods used by an organism to control and transmit how to build and maintain a new organism or portions of the organism. In other words, in the nucleus or center of a cell in an animal a large part of the information need by the animal to build eyes, teeth, skin, etc. is stored in the form of genes. Genes are part of a larger structure, chromosomes. Chromosomes are passed on to the offspring of animals giving them much of the information the adult animals have. Genes are made up of a chemical language that consists of four letter words, which in turn describe much of the how and when of making the smallest parts of an animal's body.
        As we should have learned already, the genes most likely to exist are the ones that are most efficient in organizing the chemical soup that makes up the inside of a cell. In the terms I have introduced, the phase space of the chemicals that make up a cell will have attractors that tend to produce a set of 'ideal' genes. If a change occurs in a gene the attractor will try to change the gene into one of the set of genes that the phase space of chemicals in the cell produces as an 'ideal'.
        The physical characteristics of an animal are what permit it to live. In a rabbit the better the hearing, the faster the hopping, the better the camouflage make the rabbit hard to be eaten and more likely to live and reproduce. The phase space of animal characteristics has attractors that produce better animal survival. A change in a characteristic that is away from an attractor (such as a rabbit that is hard of hearing) will not exist for long.
        Now the hard part. The phase space for animal characteristics is not the same as the phase space for genes. Together they form a new phase space with a new set of attractors. If our bodies didn't have to worry about the phase space of our genes and positive feedback our lungs would not have used the same piping that we use to eat with and people wouldn't die from choking. We needed lungs to breathe air. Evolution had to use the genes present in the evolving organism. The gene phase space was stirred and added to the existing piping for the stomach were the lungs.
        The phase space for genes on this world favors multi-purpose limbs. Escaping or hunting from the air has many advantages so flight has been developed at least four different times in the history of the world; birds, mammals, insects, and fish. Each time using a limb. But balloons are more efficient flyers. You float in the air like the spiders in 'Charlotte's Web' and not waste energy beating your wings. Some argue that wings are prevalent from positive feedback, I feel it has more to do with the phase space for genes. Feet, claws, hooks, fingers, wings all variations of the same type of genetic code. Genetic phase space leans (attracts) toward limbs. Characteristic phase space leans towards a use, flight. The result is the unique sets of different types of limbs from a similar genetic source.
        So now we know that we can not always reduce a problem to a single phase space but have to take into account the possible overlapping between multiple spaces. But still doesn't this make sense so far, and doesn't this give us a handle on solving the previous unsolvable?

6

        Have you every watched a flock of birds or a herd of animals? Many times they seem as if the herd or flock is a complete animal by itself. The marvelous movement of the herd as it encounters obstacles used to be impossible to reproduce. A few years ago a couple of computer programmers made a computer creature. The creature was made to want the company of creatures of its own kind. It was also given a desire not to be too close to its neighbor. The creature was finally given a need to travel somewhere such as a food source. When the program was run the creatures moved as a herd. Given the right obstacles just about any pattern of herd behavior could be reproduced with just these three factors (close, but not too close, and a place to go).
        Patterns once thought impossible to reproduce are now done with a simple complex model. Why does it work? Similarity across scale. What does it mean? Models, especially self-learning models, can now be used to explain non-linear problems.

7

        Genetic machines and programs are techniques to find answers to complex problems. The interesting thing about these techniques is that the user has no way to know how the programs work. In fact one of the strengths of these solutions is that the person using them has no way to bias the problem solving technique.
        We solve complex problems all the time. We therefore have developed favorite ways of attacking these problems. A problem you are working on might be unique to you and if the attempts to solve it use non-bias methods the problem should be easier to solve. Another reason to use non-bias methods is the chance that the method used to solve the problem can be more efficient.
        You start to solve a complex problem with genetics by first defining a successful outcome. Let's pretend that you are wanting to heat and cool your house using a computer program. You would define a set of optimum climate settings for each area of your house, bedroom cooler at night, temperature lower during the day, higher in the morning, et cetera. A successful outcome would come close to meeting those requirements while using the least amount of energy.
        The genetic program we are going to breed for the job would be made up of a set of instructions and sensor readings, such as turn on bathroom heater for ten minutes when temperature is sixty-five degrees. The variables in this problem would then be encoded in a portion of the program you could think of as the gene for this portion of the house. This example could be B-65-10 for bathroom at sixty-five degrees for ten minutes. We would make a number of different programs that would control the same example. The codes for the other programs could be B-66-10, B-65-9, B-68-5, and so on. All of the programs would be run and the out-comes would then be judged on how successful they were. Lets' pretend that the most successful out-comes for this set of programs were B-65-10 and B-68-5. The non-successful programs would then be dropped for the testing while the successful ones would be allowed to breed. The offspring from B-65-10 and B-68-5 could be B-65-5, B-68-10, B-65-8, B-68-8, B-66-8, etc. As you can see the genetic code for the program would be mixed using coding from the two successful programs. This breeding could be done as in the example as either just the exchanging of the original codes or with some averaging system or both.
        The next step in the process would be to run the test again with the original two successful programs and their offspring. A random generator would be included in the testing. This random generator would change the code arbitrarily on one of the offspring after every ten tests or so. Depending on how complex the problem is the resulting genetic programs would be successful in controlling the environment in your house after a series of generations of mating.
        After the program is installed in your home, tests at a longer generational period would still be done so that the program could adapt to any changes in the house's environment. Besides genetic adaptation by definition is an ongoing process.
        The system sounds wasteful and unnecessarily difficult to run. But the genetic codes find unthought of relationships. The bathroom walls could be next to a hallway and a bedroom. A one degree change up or down in either of those locations could save twenty dollars per month in the heating of the bathroom. An idea a simple as the adjustment of neighboring room temperature would be virtually impossible to check using ordinary means, but is automatic using genetic codes.
        You might think that once the programs are designed that you could just replicate the successful program in other houses. That might not be possible. Remember that the feedback is a one way street. The linking of the room temperature between the hallway and the bathroom could occur in the third generation and then virtually disappear in the detailed genetic code by the twentieth, but the pattern in the genetic code is still dependent on what happened in the third generation.
        Interestingly enough if this method is used twenty times to create genetic control programs for your home, you would get twenty successful programs, but there could be any or all of the resultant programs with different genetic codes. This is something that bothers many classically trained scientists, engineers, and mathematicians. How can you have different successful programs? Classical training says that there is only one optimum answer. With non-linear problems and feedback you get many. You just have to consider how many successful animals eat grass. Does anything make one animal better than another?

Summary

        Complexity is a unique wonderful science to explore. I used biological examples here hoping that they would be more universally known, but similar examples could have been done using social or historical systems. The biological examples are used widely in explaining non-linear problems. The biological sciences have the benefit of being more extensively penetrated by non-linear methods at this time. I avoided social examples because of the difficulties of separating our own cultural bias from the discussion. Much more can be said about the models and other techniques used to find the patterns of non-linear problems, but this is an introduction to the terms and ideas used. It's time to go on to the last technique.
back to the intro        next section fuzzy logic

Back to the Keep's Gate