Fuzzy Logic
1

        The name fuzzy logic was first used by Lofti Zadeh in the 1960's. He used the name as a challenge to the logic that the Western civilizations have used since the time of Aristotle. The ideas of fuzzy logic have been around for years. What is new is the formalization of these ideas into a mathematical type discipline that can be used to solve problems. This has been done over the last century with the majority of the work being done only in the last few decades.
        Unlike Aristotle fuzzy logic acknowledges the fact that nothing in the real world is always true or false but shades in between the two extremes. That our thoughts and words use this fact to group things and increase the information stored in them. And that is how we can survive in a non-linear system were massive amounts of information has to be quickly integrated into action.

2

        I have a favorite analogy for understanding the amount of information that a fuzzy statement can transmit. I have two curtains.
        Behind curtain number 1 there is a football player. This curtain operates in the world of absolute truth. What can you tell me about the player? Is the player boy or girl? Young or old? Big or small? Can you tell me anything about the player other than he or she or it plays football? Nothing. We have struck a dead end. We have learned only one thing. We know it a hundred percent for sure, but only one thing for sure.
        Behind the second curtain is someone who 'looks' like a football player. This curtain is in the real world of fuzzy logic. What do we know? The player is probably a boy. Age between late teens and middle thirties. Size should be large around the upper one hundred to three hundred pound range. He should look athletic and be wearing athletic type clothing. Anything else? Wait! Do we know if he plays football? No, we don't know for sure if he plays football. But look at the massive amount of information we got from the fuzzy curtain. None of it is known for sure but look how little we learned using the absolute truth of math or what we call formal logic.

3

        Some people will tell you that fuzzy logic is just probability in disguise. Bart Kosko's parking lot should tell you the difference. Who is Bart Kosko? You will find out more about him later.
        Pretend that we have an empty parking lot of one hundred spaces. You pull in and park. Probability will tell you that each space has a one- percent chance that you parked in it. Fuzzy logic would say you have one percent of your car in each parking space. They are close in meaning but not the same. Think carefully about the difference in statements.
        Now let's get a little more realistic. Assume you pull into the lot and park in the first space. As what usually happens, you were thinking of something else when parking and when you leave your car you discover that you have part of the fender or about ten percent of your car in the second parking space. Fuzzy logic would then say that ten-percent of the car is in the second space and ninety-percent in the first. Probability would say the car is ten percent completely in the second space and ninety percent completely in the first space. Now can you see the difference between the two ideas? Fuzzy logic matches closer to what we know the real world to be like. Since it matches the real world closer it should model the real world closer.

4

        Another common way of understanding fuzzy logic is looking at a person's height. If you use a standard mathematical logic system you need a cutoff number. Using standard logic you decide that anyone over 5' 11" is tall. Does it make sense to call a person 5' 10.5" short? Wouldn't you need separate cutoff numbers for different sexes, races and ages? A 5' tall first grader would be considered tall by most people.
        Doesn't it seem by this argument that we have decided that most people are both tall and short to a degree? What fuzzy logic does is take a measurement and notes the degree of the overlap. If you are looking at tall and short people and you have someone 5' 10" in height he might be thought of as 80% tall and 20% short. A person 4' 10" could be thought of as 80% short and 20% tall. This form of weighted averaging is the strength of fuzzy logic. Using proper techniques fuzzy logic can be used for logic systems, decision trees, cognitive maps, and neural nets. It could even be used as just a more accurate way of inputting information into the problems that we have already done.

5

        Many people would note that fuzzy logic sounds good, but how is it being used. A good example is a fuzzy washing machine. Using yes and no logic to make a washing machine that would automatically handle all the controls on a load of wash, would add hundreds of dollars to the cost of the machine. Dozens of special sensors and the equivalent of a small computer would have to be added to the machine. The fuzzy washing machines being sold in Japan for the last few years cost about twenty dollars more, use a handful of inexpensive sensors and a small logic chip. All you have to do to use the machine, in many cases, is put the clothes in and turn it on.
        There are currently hundreds of products using fuzzy logic ranging from cameras to cars. Fuzzy logic is just starting to be used for other non-linear problems. Most scientists refused to look closely at the logic, when it was first talked about. The ideas seemed too radical to them. It took engineers first in Europe, but mainly in Japan to start using fuzzy logic before scientists started to take it seriously.

6

        Using fuzzy logic to solve a problem is very straightforward. There is nothing difficult about the steps. Unfortunately, since we are not used to using fuzzy logic, to completely map out a problem would require about a half a dozen pages of explanation. Instead I will set up a solution so you will be able to recognize how much it can simplify a common non-linear control problem.
        You have an enclosed porch that gets too hot in the summer. You, also, have an electric bill that is higher then what you would like. You decided to install a variable speed fan with a thermostatic control. A neighbor had installed a similar fan last year. When visiting you noticed that the neighbor's room temperature would vary greatly between fan settings. You decide to buy a fuzzy control system for your fan.
        The fuzzy thermostat has five temperature sensors that can be set. These five temperature settings match with five fan speed settings.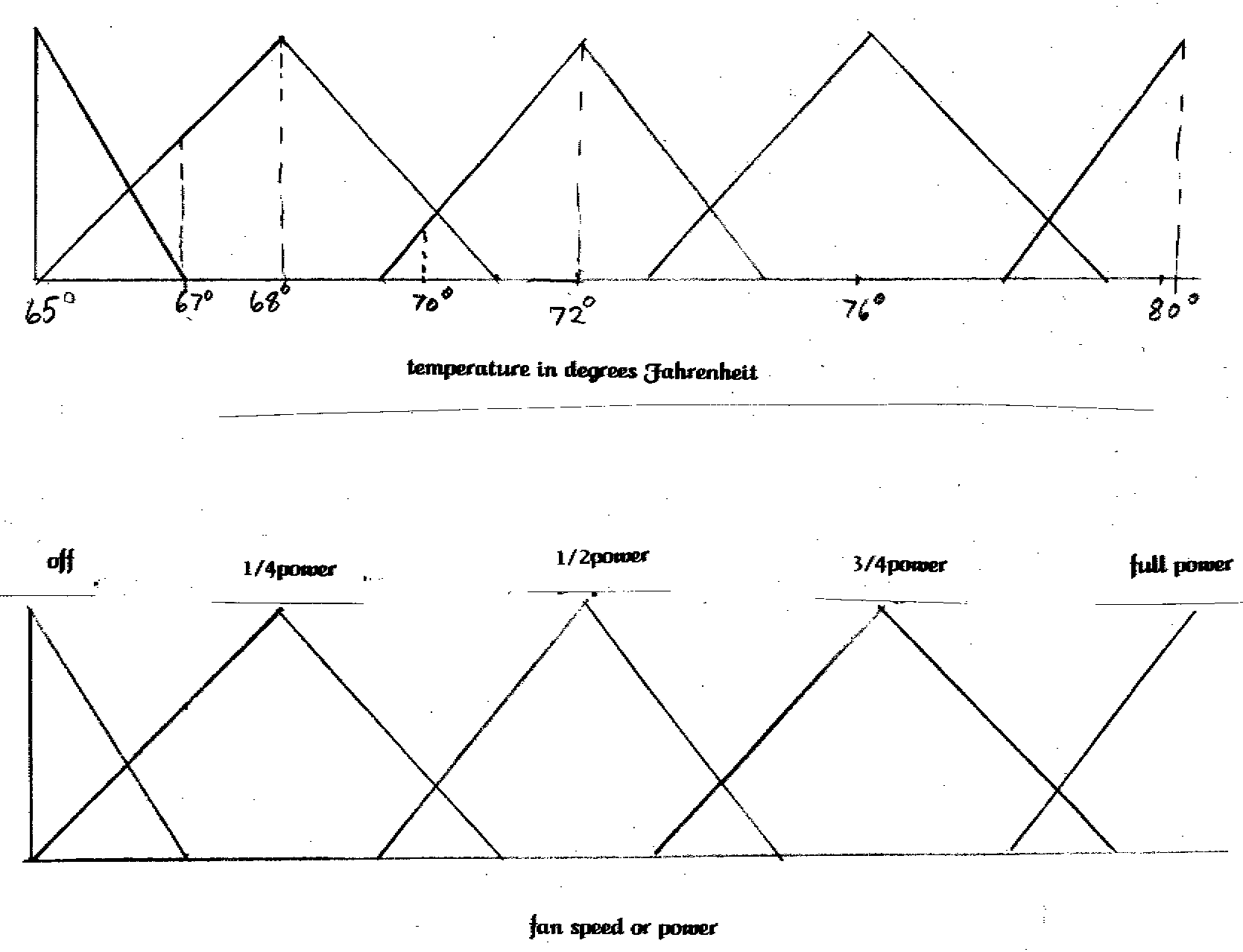 Notice that instead of having an on/off setting for different temperatures you have a triangle. Let's see what will happen at the different temperatures. At 65 degrees the fan would be off. At exactly 68 the fan would be running at 1/4 power. At 72 it would be at 1/2. At 80 it would be at full. Now lets check what will happen at the in between temperatures. At 67 degrees the temperature intersects the leg of the 1/4 power triangle at a little over half of the full height of the triangle so the fan will run at about half of 1/4 power or a little over 1/8 of full power. At 70 degrees both the 1/4 and 1/2 power settings are partially activated. The fuzzy logic chip running the thermostat makes a weighted average of the two settings using pre-made rules and produces a fan speed between the two power settings.
        As you can now see the cooling fan that is controlled by a fuzzy circuit produces a gradual change in cooling speed. No highs and lows or the on and off of what we consider normal cooling devices, but smooth gradual change. The information used to set the fan was analyzed from the range of temperatures, 65 to 80, not just a single temperature on the control switch. If the thermostat was the kind that you normally have used in your house, it would only adjust the fan speed if the room temperature passes a set point. It could not make adjustments for how much over the set point the actual temperature was. Since the fuzzy logic control does make those adjustments, it is much smarter.
        If you carry these ideas further you can solve any non-linear problem using fuzzy logic. Using fuzzy feedback loops you can design neural nets that mimic brain functions and cognitive maps that can analyze complex problems such as stock market trends.

7

        Cognitive maps are a wonderful way of solving complex problems with many dependent variables. The usual way of solving these problems was with something called games theory. Both methods use techniques that are fuzzy in nature. The big difference between the two methods is that game's theory uses a decision grid with a non-fuzzy result. A cognitive map uses a network with a pattern for the answer. Cognitive maps are hard to make, but once made give quick results.
        Since maps are hard to make accurately lets look at just a portion of a map. Let's pretend that we have a thirty thousand-acre national forest that we are going to try to manage. We would like to introduce a population of wolves into the forest. Our current management has produced a stable population of animals over the last ten years. The first step would be to create a flow chart showing the feedback that occurs between the various animals, plants, and humans. Let's limit ourselves to just the immediate feedback of the deer population.
        At the top of the paper we will write two words, wolves and hunters with the word deer just below and circle them. From the wolves we will draw two lines to deer and one to hunters. The one line to the hunters will be labeled with a negative sign and a value to indicate the degree the number of hunters would be reduced. In this case it would be slightly decrease or a number value such as 10%. One of the lines to the deer would be labeled with a negative as well and a value such as very slight. This number would indicate the negative impact on the deer population by the wolves. The final line from the wolves would have a positive sign and a value such as a slight increase indicating that since the wolves eat mostly weak and sick animals the deer population would improve by being healthier and more productive. From hunters would be a line to the deer with a negative sign and the number such as 20% indicating the hunters being the major factor culling of the deer herd. From the word deer would be two positive lines one to the word hunters and one to wolves. Lets pretend that the line to hunters has a value of 10% meaning that if the deer population changes upwards the hunters would increase by 10% and if the deer population drops the hunters would decrease by 10%. Let's label the feedback to the wolves at 5%.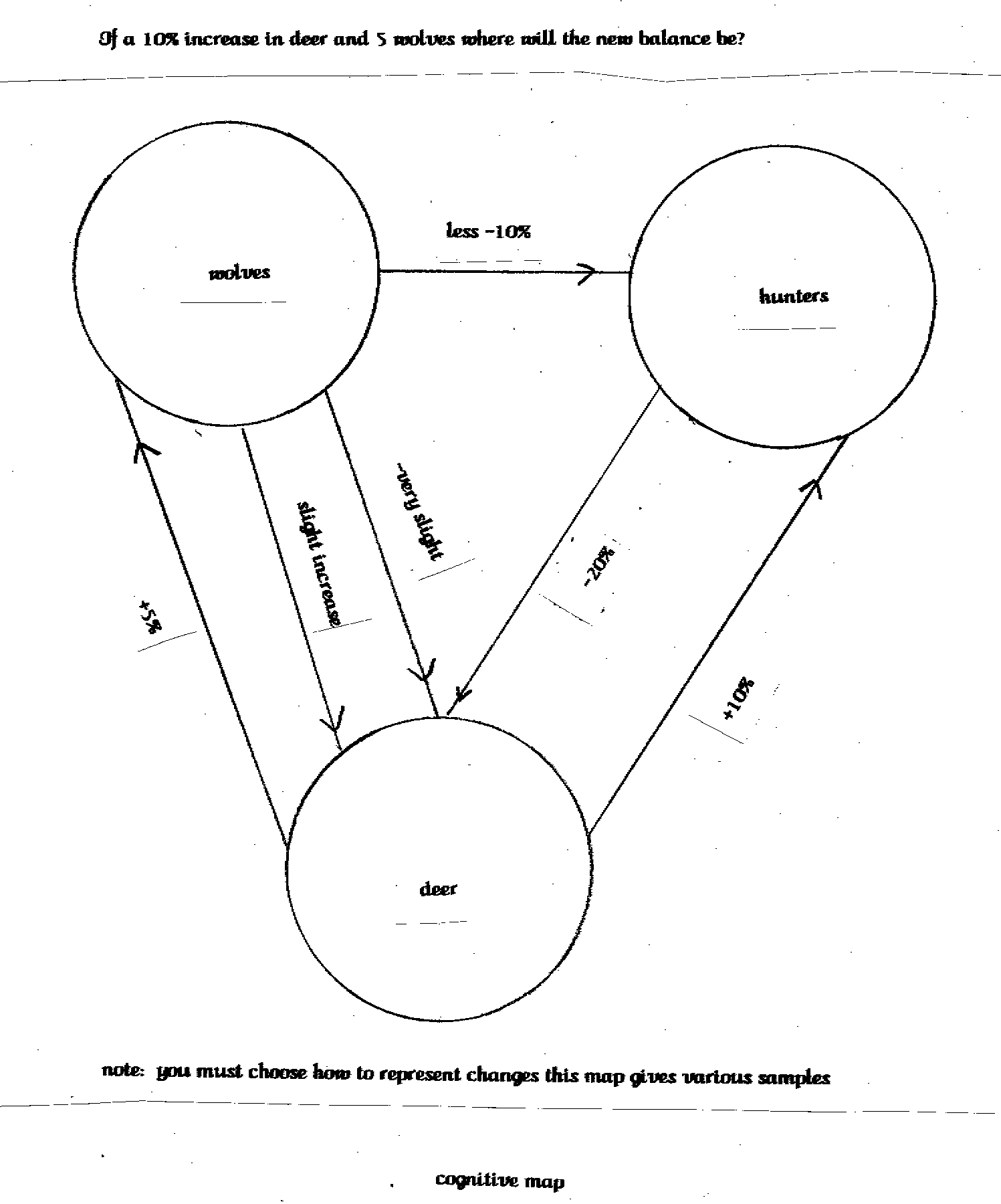
        Each circled word indicates a node with the lines showing the feedback between the nodes. The actual numbers would have to be found by study and that the nodes in an actually working map would be more numerous with additions such as food supply, etc.. The map is used by testing changes in the system. Let's say that the deer population increases by 10% because of an unusually mild winter so you try adding a pack of 5 wolves to the park. The feedback between the nodes starts working until the system stabilizes with a particular set of feedback lines activated between the nodes. The numbers at the nodes would also change indicating what the new balance between the hunters, deer, and wolves should be to keep the system stable.

8

        Although the workings of cognitive maps can be interesting, this is after all an introduction to the field of non-linear dynamics. I would not even have introduced mapping if it didn't serve as an excellent introduction to neural networks. Neural nets are one of the most used methods of trying to impart artificial intelligence in a computer.
        A neural net is just a feedback net with a set of nodes. The lines into each node are analyzed as to their combined value. After a certain threshold on input strength is met the node fires a pulse along its output lines which feed back into the net. The resulting lines will then form a pattern between the nodes. The next few steps in designing neural nets can be confusing for most people so I will not do them. By now everyone reading this should know the answer on the final step of how neural net works. That's right the resulting feedback patterns in the networks will stabilize. The pattern between the nodes is the answer.
        How does this work? Pretend time again. Let's say we are going to construct a neural net for one of the most common problems with working with machines, shape recognition. We are going to have the machine distinguish between two objects, one oval in shape and the other rectangular. The machine will place the object on a tray made up of a ten by ten grid. Each of the one hundred squares making up the grid will have one switch that will be connected to a node. All one hundred input nodes will be connected with a simplified five by five grid that the computer will read. If the pattern on the output grid becomes an 'I' the computer will sort the object as a rectangle. 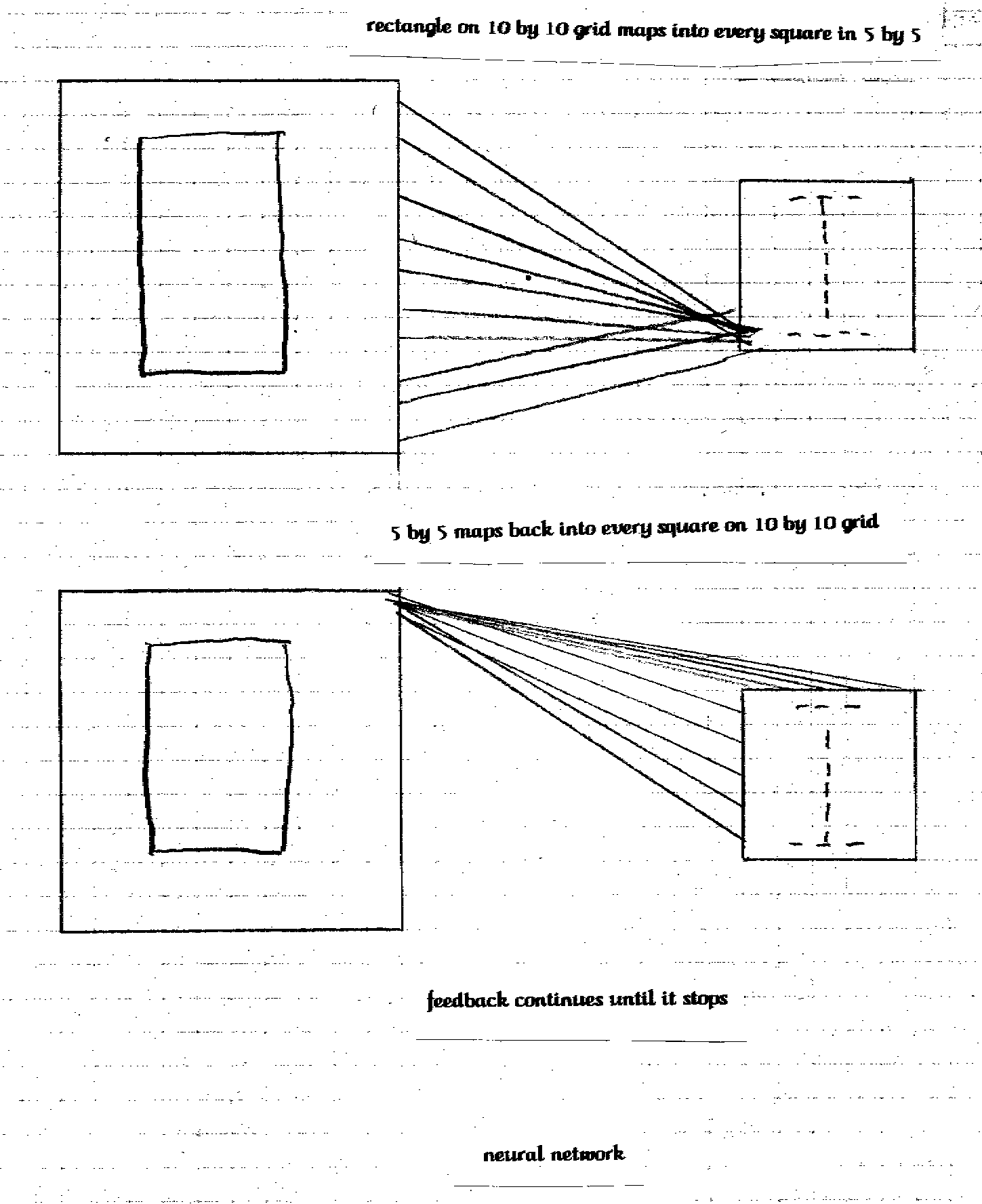If the pattern on the output grid is an 'O' then the object is and oval.
        The key on how the neural net works is the network of lines between the two sets of nodes. Every node on the input side will have one line leading to a node on the output side. Therefore all one hundred input nodes will feed information into each one of the twenty-five output nodes. The twenty-five output nodes will then feed information back to each on the one hundred input nodes.
        The neural net will be initially programmed with the two shapes by placing a sample of an oval and a rectangle on the input grid. The output grid will have the 'O' and 'I' placed in it respectively. The pattern of lines between the nodes will then be programmed.
        The system can start its distinguishing between shapes when an oval is put on the input tray. The input grid will fire its information to the output nodes. Then output nodes will then fire back to each of the input nodes a pattern that is determined by the coding of the original programming of the network. The feedback between the nodes will fire back and forth until an output pattern stabilizes. As many as 40% of the switches can be set in a different configuration and the neural net will still recognize the object in the tray as an oval. This means that the machine will now be able to recognize a wide range in size, shape, and orientation of the ovals. When the rectangular shape is added to the system the number of switches that can be set differently will of course drop. The neural net will recognize the difference between an oval laying on its side and a rectangle with less then 40% of the switches scrambled, but not by much.
        Why is this system called a neural net? We think this is the basis of how our own neural networks work. We have known for years that the brain stores and processes information in the patterns of neural energy feeding through pathways between nerves. We also know that an individual nerve can be damaged, but the information stored in the network of nerves is still retrievable just as when the individual switches in our computer nodes are set differently. Finally the organs that we use for sensory input such as the eyes have nearly as many nerve fibers going to them from the brain as going to the brain.
        The neural net I described here was for sensory input but the same methods can be used for a self-learning machine. This means that when the problems with neural networks are solved (The biggest one at this time is how to reduce the number of lines between nodes and still store detailed information.) a non-linear system can be solved by setting a self-learning neural network on the problem.

Final Summary

        I hope anyone who has studied these fields forgives me for being this fast and loose on my definitions and explanations. Now the novice to the realm of non-linear problems can finally understand those references in 'Jurassic Park' or realize that the government used the argument of positive feedback (in economics it is called increasing returns) to block the sale of Quicken to Microsoft.
        Articles and passages about non-linear problems appear in popular literature on a daily basis. There is usually a major argument in Congress every month swirling around a non-linear problem and the technical information about it; the economy, pollution, regulations, cultural control. Just listen to the catfights that occur when a single slogan congressman tries to change a non-linear social problem such as welfare. That's right folks! Except for a few academics just starting to explore the issue, no one has any idea what will happen when things are changed. Just imagine the fun you will have watching positive feedback operate, either fighting the change or creating a new stable cultural condition.
        For those interested in finding out more about non-linear problems, you could start by checking out your local college. Unless your local college is a large University don't ask about non-linear problems, ask about the topics I covered here. Most local colleges can steer you in the right direction when you inquire about Fractals and Chaos. The other topics are new enough that it can be daunting to find a college instructor versed in those areas.
        For the layman you can check popular magazines. Books such as Fuzzy Logic by McNeil and Freiberger, Chaos by Gleick, Fuzzy Thinking by Kosko, and Complexity by Waldrop can start you on your way. If you can handle a tough read The Collapse of Chaos by Cohen and Stewart will give you enough information to argue with scientists about anything from the second law of thermodynamics to genetics.
        If you have a computer, there are hundreds of sites on the Internet about these subjects. There are programs such as Fractint that let you explore fractals. There are bulletin boards about artificial intelligence and neural nets.
        For someone with a light background in math and plenty of time, there is a series of high school math books called Fractals in the Classroom. There are plenty of books on these subjects that require a strong background in math. Some like Fractals, Chaos, Power Laws require heavy math and computer or binary math skills to read.
        The only topic that you will have a hard time finding a variety of information on, unless you can read Chinese and Japanese, is fuzzy logic. Here you are limited mostly to materials written by Kosko and Zadeh at this time. Zadeh could be considered the father of fuzzy logic. Kosko is one of the top fuzzy theorists in the world and one of its strongest advocates.
        Even if you don't have the time to learn more about non-linear problems, it doesn't mean you have to ignore them. Much of the best work in this field has been done when two or more people collaborate on a project. Find a friend and start to talk. You will be surprised at how fast you will become skilled with these problems. A good place to start is with a historical event. Since you know the outcome, it is easy to check your work. A word of warning, try not to let your knowledge of the outcome color your analysis of the problem.
        Have fun and prosper and may the joy of being non-linear always be with you.
.
back to the intro        

Back to the Keep's Gate