Chaos
1

        Chaos is the currently in vogue sexy math theory. It is used, many times inappropriately, to explain or argue points and opinions. It is a formal large-scale attempt to understand non-linear problems mathematically. It is important, because just about everything that we, in real life, are involved in is non-linear.
        What is now considered Chaos theory in common vernacular is not the same as the official starting version of Chaos. Many mathematical attempts were made at understanding non-linear problems. Some had fascinating names such as Catastrophe theory (now usually called bifurcation). Others were never formally named or codified into a theory. Most of these attempts at understanding non-linear problems have been slowly merged with Chaos. Others are sitting at the fringes waiting for a home somewhere. These fringe ideas have been alternately used to support or tear down various non-linear ideas. I will try my best to avoid these fringes. These ideas will eventually find a home, but all you need to know now is that they exist.
        Let's start by looking at the known characteristics of Chaotic systems, then look at some examples of those systems. At first these characteristics will seem confusing, until you realize that just about everything that you, as an individual, interact with have these characteristics. You will see these features everywhere.

2

        Chaos is not chaos everywhere. Portions of a Chaotic system are well behaved or linear. In fact what we consider standard science and math are just the linear portions of a much larger non-linear systems. The well-behaved portions of Chaos can occur at any time during an examination of such a system. Chaos also results in portions of a system being only 'slightly' chaotic.
        In the math and science classes you took in school nearly every word problem had some limiting factors (i.e. ignore friction, assume elliptical orbit, consider only two objects at a time). You ever wonder why? Chaos! When those factors are added into the equations you can get more than one answer. An arrow shot up in the air and no one knows, for sure, where it will land. (Close does not count.)
        If the planets' orbits are elliptical, why does NASA make mid-course corrections when it sends out a space probe? Because whenever you have more than two attractive bodies (i.e. gravity) you've got chaos. The interaction of the gravity fields in our solar system makes precise prediction of a probe's path impossible. Course changes have to be made to compensate for the so-called drift.
        Go out on a lake in a boat. Closely watch the waves. Any day on the lake will work, but the days with a sharp chop to the waves delivers the easiest viewing. If you look carefully across the waves you will always be able to see smooth and rough surfaces. Sometimes the smooth surfaces will even be part of a larger wave. The waves in areas will sometimes form patterns. Some patterns will have a regular wave breaking ashore, one after another. Another pattern will be a large wave then a smaller one. Another pattern will have one large followed by two small waves. And so on. Finally there will be a spot that the chop is so irregular that no pattern can be found. Chaos! a system that is both regular and irregular.
        At this point Chaos takes two basic approaches to solving the problem. The first is the one preferred by most mathematicians. Find the simple equation that generates the pattern. The idea we used before when making fractals. The other is to study the pattern itself.
        What good is studying the pattern? If your boat just capsized off the California coast and you were being washed ashore by the surf, the pattern of a large wave followed by three small waves would become very important to you.
        People are used to being given exact answers to problems. But remember we are looking at non-linear problems, the problems that have more than one good answer. A pattern of how the answers occur even for just a portion of the curve or problem becomes important.

3

        It would probably be best to define some terms used with non-linear systems. Let's start with phase space.
        Pretend that we have a box. When you shake the box a pair of numbers come out. You want to study these number pairs. Every pair of numbers that come out of the box could be called an iteration. It would be nice to use a representation that would be able to show all the possible combinations of numbers. We want to then show on this representation our actual number pairs. This representation is phase space and the graphing of actual numbers is how it is used.
        Now back to our example of number pairs. In your high school math classes you used a phase space to understand pairs of numbers. Remember the old X Y coordinate graph you always hated to use? Two perpendicular lines were used to define a plane. The X line was used to represent the first number of a pair of numbers. The Y line was used for the second. Any combination of real number pairs could be graphed on the X Y coordinate plane. Since all possible combinations could be graphed, the X Y plane became the phased space for pairs of numbers. When you graphed the actual pairs of numbers on the phased space you could discover all sorts of interesting things about the pairs, some pairs formed lines, some circles, others open curves, and so on. You never knew that you were working with phased space every time you made an X Y graph. Did you?
        Why do we now add the idea of phased space to what we have previously called graphing? Before you would graph an equation to study the original equation. In non-linear systems you are reversing the role. You create a phase space to study the behavior in phase space. As you will see later many non-linear systems have more then one phase space. That means if the non-linear problem is too hard to solve in its entirety then you could possibly solve it for just one of its phase spaces.
        If you are still having trouble understanding why phase spaces consider a three-dimensional non-linear line. If it were plotted on a graph you would need X, Y, and Z coordinates. And if it is a very broken line or fractal you would have problems seeing what is happening to the curve when it folds behind itself. The solution will be to just look at the curve in, let's say, just the X phase space. The resulting graph won't show the whole curve but all the actions of the X coordinate can now be seen.
        When you study non-linear (remember they are not simple lines) systems in a phase space you are more interested in the controlling features then the lines themselves. An attractor is a point or area in phase space that seems to suck in the solutions of a non-linear system when the equation you are using for the non-linear system is iterated. (The usual way you hear about attractors is with the adjective 'strange'. This adjective seems to be added to separate the word from other attractors in the real world and not in phase space. There is a technically correct definition of strange attractors but mine is good enough for now.) The large basin looking area of the Mandelbrot set is an attractor. A repeller is a point or area in phase space that solutions graph away from. Again on the Mandelbrot that would be the area outside of the boundary curve. It is interesting to note that there is frequently a relationship between attractors and repellers. If a solution is going away from some point or area it has to be going to another. In the Mandelbrot set the area that is being repelled is being attracted to the infinite.
        A fixed point is a point in phase space that the solutions never escape from. Often in the middle of an area of attraction there is a fixed point. It acts the same way as a black hole in space does. If a solution of a non-linear system comes too close to this area of phase space it becomes sucked in, spiraling in towards the fixed point until it becomes locked in, never escaping.
        If there is an area of phase space that your solutions seem to bounce around, that area is described as periodic. A periodic orbit can be made up of just two numbers or solutions that are alternately correct or derived after each iteration. There is no limit on the number of possible solutions that make up a periodic orbit.
        The final definition I will give you at this time is bifurcation (also known as a catastrophe). When you plot your solutions of non-linear problems, many times they will start as a simple line. (Remember this is the area where the math and science, everyone is familiar with, occurs. All the formulas you learned are just the very small portions of non-linear problems that have a single answer.) At some time later the plot will split or bifurcate. (This is how it received the other name, catastrophe. This is where the breakdown of our old math and science started and where the breakdowns in natural systems occur.) In a very short time the lines will split or bifurcate again.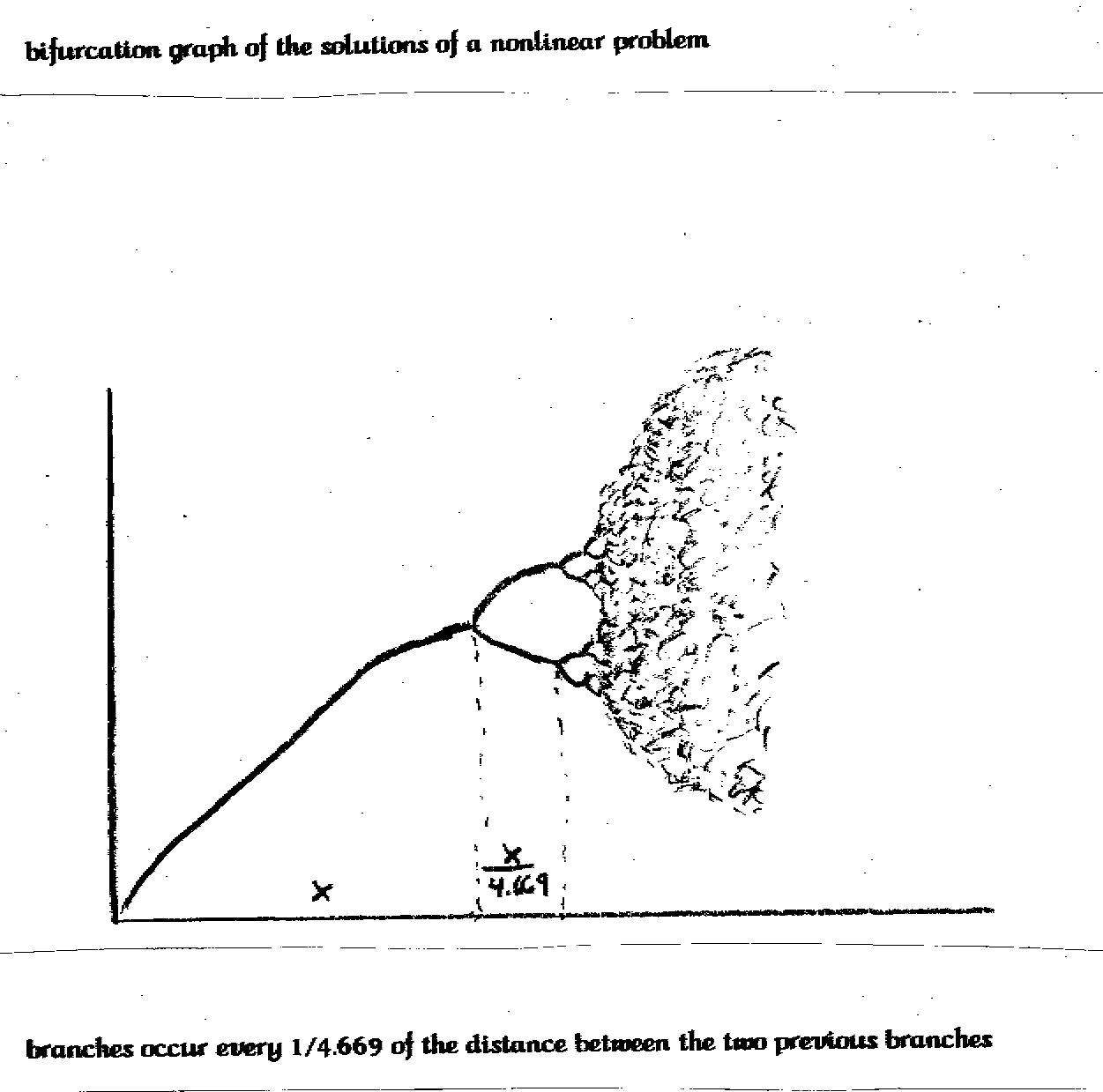 A man by the name of Feigenbaum discovered that the distance between each bifurcation of a category of non-linear equations follows a simple ratio. The ratio or distance is 1/4.669. This strange ratio seems to hold for any non-linear problem category. In fact if you look at the picture of the Mandelbrot set each circular basin along the axis from right to left is 1/4.669 the size of the previous circle. (For those who just have to know what category Feigenbaum's ratio hold for it is for normal or a one-hump distribution. This is probably the most used category of non-linear problems at this time.)
        There is a linkage between periodic orbits and bifurcation. They are different ways of looking at the same features and tell different things about what is happening to the non-linear problem. If you are interested in the linkage, try to plot in phase space an equation that bifurcates and compare it with an orbital or iteration plot.

4

        After all those nasty definitions it is time for a break. Let's talk about butterflies and their affect on weather.
        People in the United States are interested in hurricanes. Especially those people who live on the East Coast. A few years ago the weather service was able to trace back a hurricane to a starting point. They were able to trace the storm back to an area of dunes in the Sahara Desert.
        There are thousands of dunes in the Sahara Desert. Every day when the sun warms the dunes a warm air bubble forms over each dune. Just one of the thousands of daily warm air bubbles may eventually become a hurricane. What could happen to one of these low-pressure air bubbles to cause this? Maybe a snake crawls over the edge of the dune causing sand to fall and strengthening the low pressure. Maybe a butterfly flaps its wings. Whatever it is the low strengthens and survives the cool temperatures of night. It then continues building and drifts into the Atlantic. There the warms moist air builds the low into a tropical storm and finally a hurricane.
        This small change in the starting point of a non-linear system that makes such a large difference later on is called the 'Butterfly Affect'. I know we have talked about this feature before in positive feedback, but its importance bares this reinforcement. Just think! You could sneeze at the right time and cause a storm in Europe! And this is just weather, one of the hundreds of non-linear systems you encounter every day.

Summary

        Chaos is a mathematical attempt to explain non-linear problems. Its greatest use and benefit for those exploring these problems are the definitions of features and concepts it has prescribed. The idea that you can examine a simple pattern of a system that has too many possible answers is conceivably the strongest method of working with the majority of non-linear problems. The next section will take these ideas and run with them.

I have found a nice online book on Chaos that can continue this discussion. Chaos Hypertextbook

back to the intro        next section complexity

Back to the Keep's Gate